What are the most important Classification Methods in Machine Learning?¶

Classification is a supervised learning where the outputs belong to a discrete set of categories.

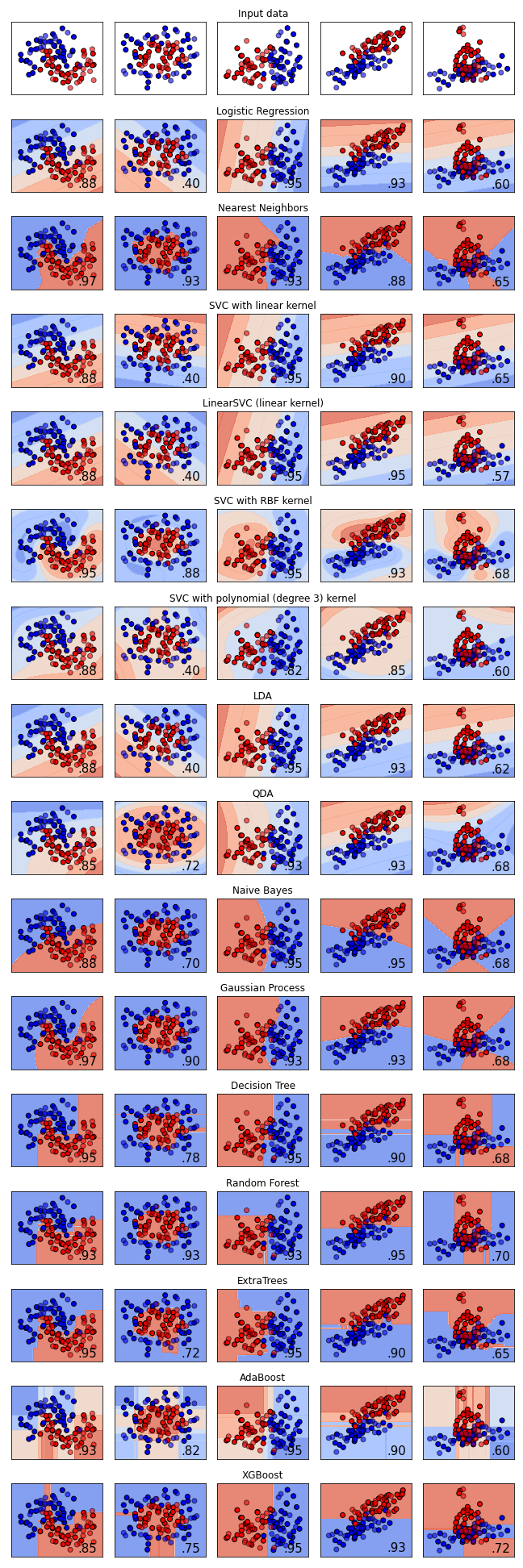
Here we include a brief summary of important classification methods and a summary chart comparing their results on a set of samples.

Logistic Regression

In logistic regression we assume that the probability of binary target is 1 is given by

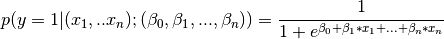
$p(y=1|(x_1,..x_n);(\beta_0,\beta_1,...,\beta_n)) = \frac{1}{1+e^{\beta_0+\beta_1*x_1+...+\beta_n*x_n}}$

In this case, the probability of target being 0 will be

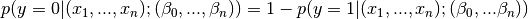
$p(y=0|(x_1,...,x_n);(\beta_0,...,\beta_n)) = 1-p(y=1|(x_1,...,x_n);(\beta_0,...\beta_n))$

We define a cost function to be minimized as

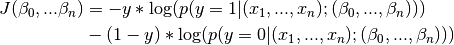
$\begin{align*} J(\beta_0,...\beta_n) & =-y*\log(p(y=1|(x_1,...,x_n);(\beta_0,...,\beta_n)))\\ & -(1-y)*\log(p(y=0|(x_1,...,x_n);(\beta_0,...,\beta_n))) \end{align*}$

Multinomial Logistic Regression (MLG) a.k.a. Conditional Maximum Entropy Model (CMEL) is multinomial version where the problem is framed as many against a reference choice.

K Neighbors

In K Neighbors method, the label of each observation is chosen as the mode of the k-nearest points in the training data.

Support Vector Machine (SVM)

Support vector machine constructs a number of hyper-planes in a high dimensional space separating the data. This is achieved by considering the function 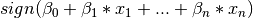$sign(\beta_0+\beta_1*x_1+...+\beta_n*x_n)$

Kernel Support Vector Machine (KSVM) applies the kernel trick to the input (i.e. a similarity function between the inputs replaces the inputs in the optimization).

Discriminant Analysis

In Discriminant Analysis we apply Bayes’s theorem such that

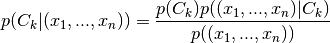
$p(C_k|(x_1,...,x_n)) = \frac{p(C_k)p((x_1,...,x_n)|C_k)}{p((x_1,...,x_n))}$

Here 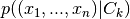$p((x_1,...,x_n)|C_k)$ is assumed to follow a multivariate distribution and the parameters are chosen according to the discriminant rule (e.g. maximizing group population density).

Quadratic Discriminant Analysis (QDA) is the resulting generic problem while Linear Discriminant Analysis (LDA) is the special case that the covariance matrix for every class is assumed to be the same.

Naive Bayes (NB)

Naive Bayes classification utilizes Bayes’ theorem together with the assumption of independence of the features to achieve a scalable classification method. In summary, the probability of an input belonging to each class is computed as

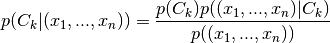
$p(C_k|(x_1,...,x_n)) = \frac{p(C_k)p((x_1,...,x_n)|C_k)}{p((x_1,...,x_n))}$

where feature independence implies

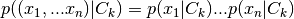
$p((x_1,...x_n)|C_k)=p(x_1|C_k)...p(x_n|C_k)$

Finally a particular distribution is assumed for each 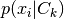$p(x_i|C_k)$ and is often estimated via Maximum Likelihood Estimation (MLE). A common choice of distribution is Gaussian distribution.

Gaussian Process

Gaussian Process in classification is used via the application of Bayes’ theorem. Here we place a Gaussian Process prior over a latent function and then squash this through the logistic function to obtain a prior on 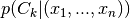$p(C_k|(x_1,...,x_n))$ .

Decision Trees

In Decision Trees the feature space is recursively partitioned such that samples within same class are partitioned together. At every step a feature and a threshold are chosen such that the total impurity is minimized. Common measures of impurity include Gini, Entropy and Misclassification.

Ensemble Methods

The Ensemble methods are used to combine the predictions of several classification methods to achieve better generalizability or robustness. In Averaging Ensemble methods such as Bagging and Forests, the results of several classification methods are averaged while in Boosting methods such as AdaBoost or Gradient Tree Boosting, several classification methods are applied sequentially.

Comparison

The chart below demonstrates the results of various methods on a number of classification samples.