What are the most important Regression Methods in Machine Learning?¶

Regression is a supervised learning where the output belongs to a continuous interval of numbers.

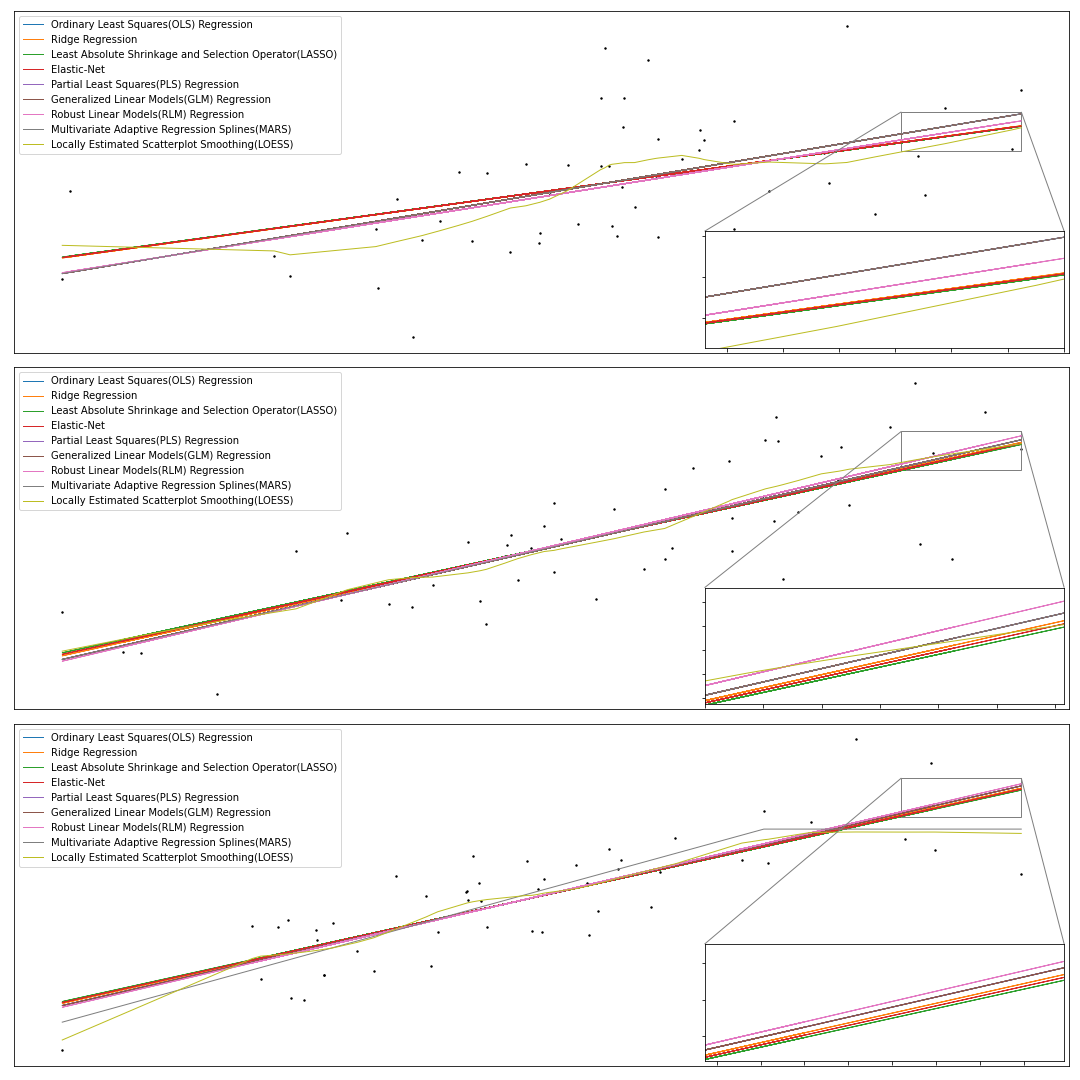
Here we include a brief summary of important regression methods a summary chart comparing their results on a set of samples.

Ordinary Least Squares Regression (OLS)

In OLS the target variable is a linear function of the features:

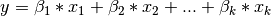
$y = \beta_1*x_1+\beta_2*x_2+...+\beta_k*x_k$

OLS finds the coefficient such that the residual sum of squares between the observed targets and the predicted ones via the equation is minimized.

Ridge Regression

In Ridge Regression a penalty function on the 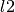$\mathit{l}2$ norm of coefficients is imposed resulting in increased robustness of coefficients to collinearity.

Least Absolute Shrinkage and Selection Operator (LASSO) Regression

In LASSO a penalty function on the 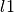$\mathit{l}1$ norm of coefficients is imposed resulting in preference to solutions with fewer nonzero coefficients.

Elastic-Net

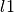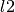In Elastic-Net a penalty function on combination of $\mathit{l}1$ and $\mathit{l}2$ norms of the coefficients is imposed where both properties of Ridge and LASSO are maintained.

Partial Least Squares Regression (PLS)

PLS aims to capture the maximum variance from input features and at the same time maximize the correlation between features and target in an iterative manner.

Generalized Linear Models (GLM)

Generalized Linear Models are extension of linear models such that the predicted target variable is linked to linear combination of feature via an inverse link function and at the same time, the square loss function is replaced by the unit deviance of a reproductive exponential dispersion model.

Robust Linear Models (RLM)

Robust Linear Models take advantage of robust criteria function to downweight outliers and estimate the coefficients on an iterative manner.

Multivariate Adaptive Regression Spines (MARS)

MARS makes use of hinge functions and a form of regularization named generalized cross validation to build a piecewise linear regression.

Locally Estimated Scatterplot Smoothing (LOESS)

LOESS estimates the predicted value based on a weighted linear regression on the fraction of total sample close to the point where the weight is tri-cube function of the input distance. This helps to reduce the impact of heavy tail noise in the data.

Comparison

The chart below demonstrates the results of various methods on a number of regression samples.