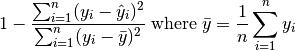How can we quantify the quality of the prediction of Machine Learning models?¶
There are a number of scores defined and computed for various machine learning problems. Here we categorize the scoring methods based on the problem category: Classification, Regression and Clustering and include the most frequently used measures.
Classification
accuracy score: fraction of the correct prediction to total predictions
precision-recall curve: shows the precision (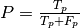 ) against recall (
) against recall (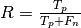 ) by varying a decision parameter where
) by varying a decision parameter where 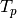 ,
, 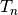 ,
, 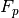 , and
, and 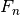 refer to the true positive count, the true negative count, the false positive count, and the false negative count, respectively.
refer to the true positive count, the true negative count, the false positive count, and the false negative count, respectively.
f1-score: f1 score is computed as 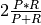 where
where 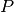 and
and 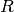 refer to precision and recall respectively.
refer to precision and recall respectively.
roc curve: shows the true positive rate (TPR = 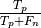 ) against the false positive rate (FPR =
) against the false positive rate (FPR = 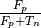 ) by varying a decision parameter.
) by varying a decision parameter.
confusion matrix: entry i,j in this matrix shows the number of observations in group i but predicted to be in group j.
Clustering
adjusted rand index: is the corrected for chance version of rand index which is a measure of similarity between two data clusterings and represents the chance of occurrence of agreements for any pair of elements.
adjusted mutual information: is the corrected for chance version of mutual information score which is bounded by the entropies of each cluster.
contingency index: entry i,j in this matrix shows the number of true members of cluster i predicted to be in cluster j.
Regression
mean squared error: defined as the average of square difference between actual and predicted output
mean absolute error: defined as the average of absolute difference between actual and predicted output
explained variance score: defined as 1 minus variance of error divided by variance of actual output, that is:
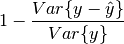
R² score: defined as 1 minus sum of squared error divided by sum of squared difference from output mean, that is: