What are various methods in Model Free Reinforcement Learning?¶

Different methods in Model Free Reinforcement Learning leverage on one or both of Policy Optimization and Q-Learning. In Policy Optimization the parameters specifying the policy are tuned to arrive at an optimal policy, whereas in Q-Learning the action-value function is optimized.

Policy Optimization

Policy Gradient

In Policy Gradient, the policy is updated based on the gradient of the expected return. The gradient is estimated based on set of trajectories that are obtained by running the policy.

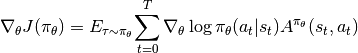
$\nabla_{\theta} J(\pi_{\theta}) = E_{\tau \sim \pi_{\theta}}{\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}(a_t|s_t) A^{\pi_{\theta}}(s_t,a_t)}$

Actor-Critic

Actor-Critic refers to the family of approached that during the policy optimization, either action or state value function is also learned. In A3C for example, the state value is learned and used as the baseline for the policy gradient update.
Proximal Policy Optimization (PPO) & Trust Region Policy Optimization (TRPO)

In both PPO and TRPO, the policy is updated to maximize the surrogate advantage. In PPO, the optimization is penalized by distance between the current policy and the updated policy while in TRPO, the KL divergence between the current and the updated policy is constrained.

Q-Learning

Deep Q Network (DQN)

In DQN, a neural network is used to learn the 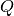$Q$ value function and experience play and periodically updated target are used to improve and stabilize the training. Here, the action is picked based on maximum 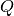$Q$ value, and the 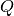$Q$ value is updated based on the observed reward based on the following equation where 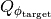$Q_{\phi_{\text{target}}}$ is copied from the main network every fixed-number-of-steps.

$\nabla_{\theta}\frac{1}{|{B}|}\underset{(s,a,r,s',d) \in {B}}{{\sum}} \Bigg( Q_{\phi}(s,a) - \left(r + \gamma Q_{\phi_{\text{targ}}}(s',\mu_{\theta_{\text{targ}}}(s'))*\begin{cases} 0 & s' \text{ terminal state}\\1 & \text{otherwise}\end{cases} \right) \Bigg)^2$

Hindsight Experience Replay (HER)

In HER, a set of additional goals are added such that the replayed trajectories have either the original goal or one of the alternative goals. HER helps to speed up the convergence particularly in the presence of sparse rewards.

Combination of Policy Optimization & Q-Learning

Deep Deterministic Policy Gradient (DDPG)

In DDPG, the 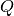$Q$ value is updated similar to DQN and the policy is updated based on: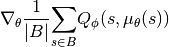

$\nabla_{\theta}\frac{1}{|{B}|}\underset{s \in {B}}{{\sum}} Q_{\phi}(s, \mu_{\theta}(s))$

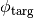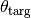here $\phi_{\text{targ}}$ and $\theta_{\text{targ}}$ are updated based on: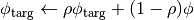

$\phi_{\text{targ}} \leftarrow \rho \phi_{\text{targ}} + (1 - \rho) \phi$

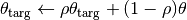
$\theta_{\text{targ}} \leftarrow \rho \theta_{\text{targ}} + (1 - \rho) \theta$
Twin Delayed DDPG (TD3)

TD3 is enhanced version of the DDPG to address the issues with hyperparameter tuning and Q-value overestimation. The algorithm learn two Q functions concurrently and uses whichever gives a smaller target value. The policy and target networks are updated less frequently and finally noise is added to the target action to avoid exploitation of Q function errors by the policy.
Soft Actor-Critic (SAC)

SAC builds on the central idea of entropy regularization and optimizes the policy to achieve a balance between expected return and policy entropy. Value function and action-value function are redefined to include the entropy reward. Update of the Q-function and policy are similar to TD3 with exception of addition of the entropy terms, the next state actions coming from the current policy and absence of explicit target policy smoothing.